前言

在昨天如果你有嘗試調整超參數並更換其他邏輯閘，你可能會發現無論怎麼調整，XOR與NXOR這兩個邏輯閘都無法正確的被預測。這是因為單層感知器的原理是在一個平面座標上畫一條直線來分割不同的分類(也就是非線性可分)，因此當XOR與NXOR的輸入對應到x和y座標時，我們會發現無法用一條線進行分割。因此今天我們將學習如何解決這個問題。

多層感知器(Multilayer Perceptron)

多層感知器(Multilayer Perceptron, MLP)能解決非線性可分的關鍵在於它引入了隱藏層(Hidden layer)，這使得每一個每個隱藏層中的神經元(Neuron)能夠學習更高階的複雜特徵，從而處理非線性問題。這個概念也就是通過增加神經網路的深度與隱藏層神經元數量，能夠大幅提升模型的表現與準確性。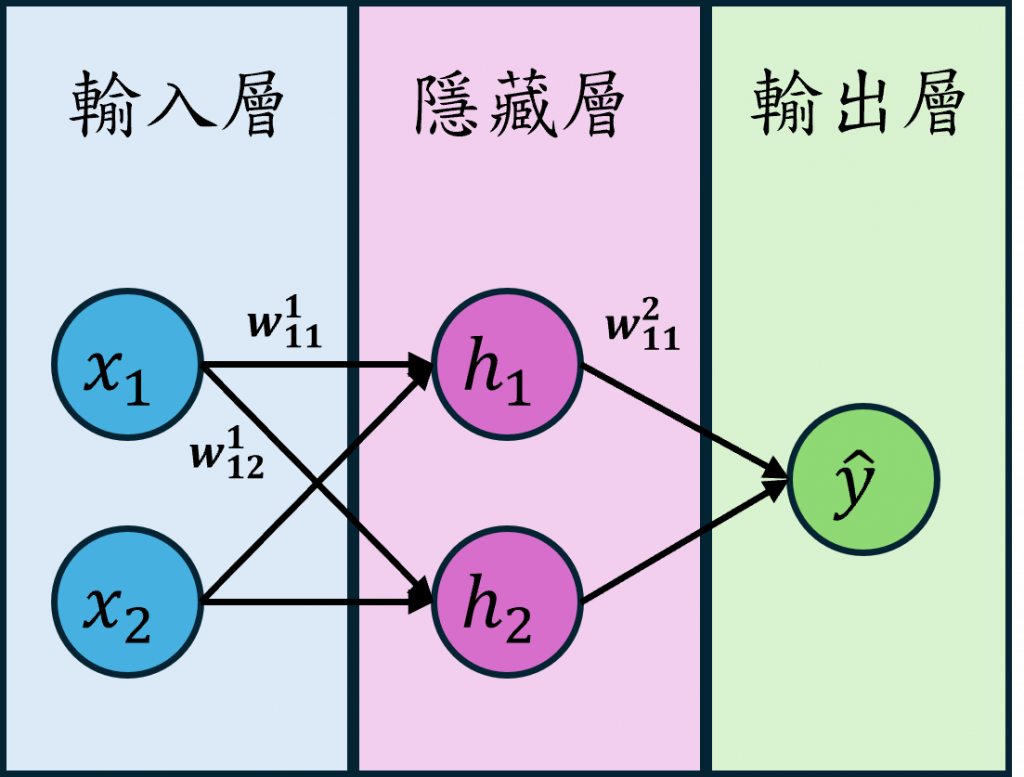

在多層感知器中通常會在層與層之間設定不同的激勵函數，將wx+b這一個線性運算轉換成非線性的結果，我們可以設定多個隱藏層經過多次線性變換和非線性激活，逐層提取更高階的特徵，現在讓我們看看圖片中的數學公式是如何計算出來的吧。

前向傳播

多層感知器的前向傳播公式其實相當直觀，其基本原理就是將單層感知器的結果不斷向後面的神經網路傳遞。因此我們首先要計算從輸入層到隱藏層神經元 h 的結果，其計算方式與單層感知器相同，都是使用 wx+b。不過為了方便運算，這裡暫時省略了偏移量。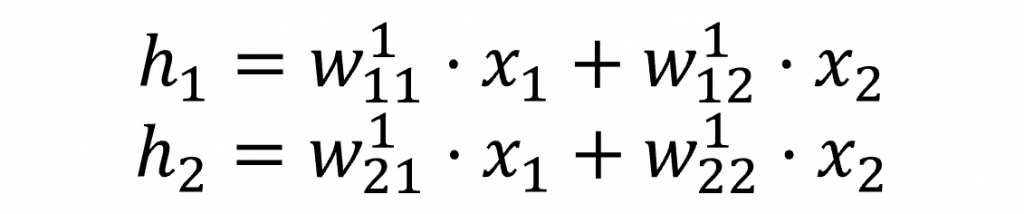

接下來我們要計算從隱藏層到輸出層的過程，我們選擇使用sigmoid激勵函數。該函數可以將數值縮放到0到1之間，這對於二元分類或一些開關控制特別有效。在這裡，我們先計算出未經過激勵函數運算前的結果z，並將其帶入到sigmoid函數中，以計算出預測輸出ŷ。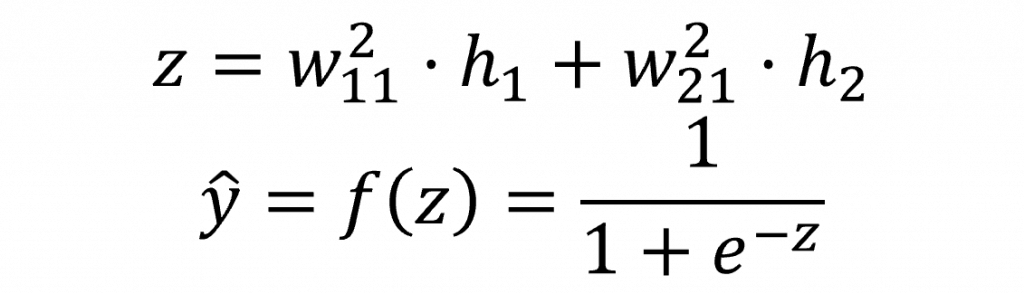

而之所以加入 sigmoid 函數，是因為當我們的計算複雜度變大時，輸出的輕微調整可能會帶來很大的變化。因此我們通過使用 sigmoid 函數來縮放其輸出數值，確保最終的損失值不會出現過大的變動。這樣在計算梯度時，變化會更為合理。以下圖示展示了 sigmoid 函數的輸入與輸出變化。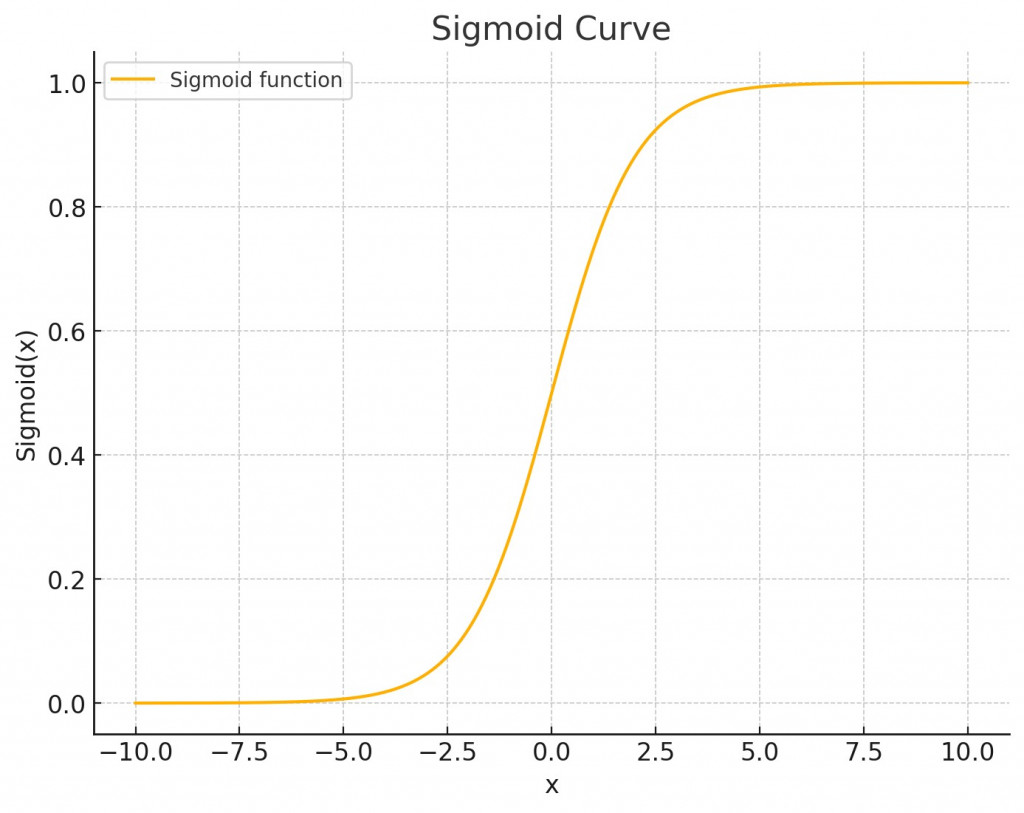

反向傳播

而在這多層的神經網路架構中其反向傳播是非常繁雜的，同樣的我們先從損失函數與預測輸出開始進行連鎖律運算，其數學式如下: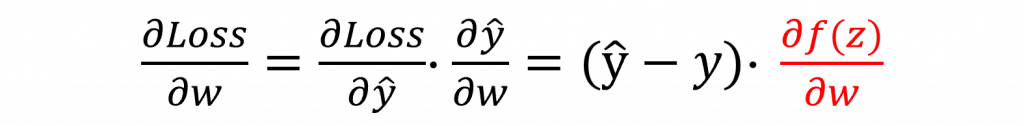

其中我們可以直接計算出𝜕Loss/𝜕ŷ的答案，但是我們並不知道𝜕ŷ/𝜕w的答案。這是因為對於𝜕ŷ/𝜕w來說，它還經過了激勵函數的轉換與隱藏層的計算。因此，我們還需要針對𝜕ŷ/𝜕w再次使用連鎖律進行展開。因此我們可以再次證明出以下的數學公式。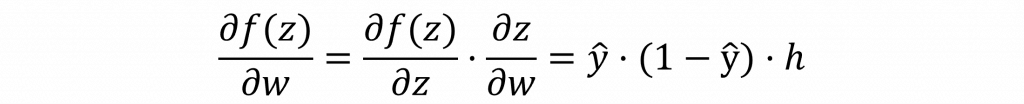

這裡計算到目前為止，我們已經能夠取得隱藏層到輸出層的權重梯度變化值，但這還不夠我們還必須計算出輸入層到隱藏層的權重梯度變化值。

因此我們需要針對每個隱藏層的神經元，計算損失值相對應的偏微分，也就是計算𝜕Loss/𝜕h這個結果。這部分的計算過程與先前類似，所以在這裡我們直接將其一次證明完畢(紅字的部分是使用連鎖律再次展開)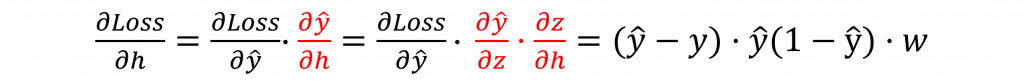

到這裡我們已經完成了整個圖片中多層感知器的前向傳播和反向傳播。可以看到當我們的神經網路越深時，其計算量和反向傳播的公式會變得更加複雜。因此在實際使用程式進行運算時，並不會真的手動計算這些反向傳播的公式，而是採用自動微分的方法來追蹤和計算梯度，這樣能更高效且準確地完成梯度的計算。

總結

我相信你今天看到這裡可能已經對反向傳播的概念更清楚一些了，但還是無法完全理解每一個數學式該如何計算。這樣其實非常正常，因為神經網路的關係過於複雜，很難一下子就掌握這些方程式之間的關係。所以當我們在計算反向傳播時，只需要記得一件事：如果我們所求的目標無法直接進行偏微分，那麼就一定要進行連鎖律展開。而連鎖律展開的相關變數，會是當前神經網路層的上一層輸出變數。